Question:
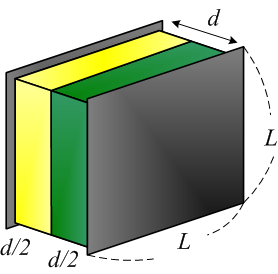 There is a parallel plate capacitor the area of \(L^2\) and separation distance of \(d\). A half of the space, \(d/2\), is filled with a material of dielectric constant, $\kappa_1$. The other half is filled with the other material, \(\kappa_2\). What is the capacitance of this capacitor if the free space capacitance is \(C_0\)?
There is a parallel plate capacitor the area of \(L^2\) and separation distance of \(d\). A half of the space, \(d/2\), is filled with a material of dielectric constant, $\kappa_1$. The other half is filled with the other material, \(\kappa_2\). What is the capacitance of this capacitor if the free space capacitance is \(C_0\)?
Answer:
The capacitance of a parallel plate capacitor is given as
\[ C = \frac{\epsilon_0\kappa A}{d} \]
where \(A=L^2\). When a capacitor does not have any dielectrics (free space between plates), it will be
\[ C_0 = \frac{\epsilon_0 A}{d} \]
We can consider the particular capacitor which is like series connection of two different capacitors. Namely,
\[ \frac{1}{C_{\mathrm{Total}}} = \frac{1}{C_1}+\frac{1}{C_2} \]
\[ \rightarrow C_{\mathrm{Total}} = \frac{C_1C_2}{C_1+C_2} \]
From the given condition, we have each capacitance of \(C_1\) and \(C_2\).
\[ C_{1,2} = \frac{\epsilon_0\kappa_{1,2} A}{\frac{1}{2}d} = \frac{2\epsilon_0\kappa_{1,2} A}{d} \]
Then, we can rewrite it in terms of \(C_0\).
\[ C_{1,2} = 2\kappa_{1,2}C_0 \]
Plug it in the above.
\[ C_{\mathrm{Total}} = \frac{2\kappa_1C_0\times 2\kappa_2 C_0}{2\kappa_1C_0+2\kappa_2 C_0} \]
\[ = \frac{4\kappa_1\kappa_2 C^2_0}{2C_0(\kappa_1+\kappa_2)} \]
\[ = \frac{2\kappa_1\kappa_2 C_0}{\kappa_1+\kappa_2} \]
