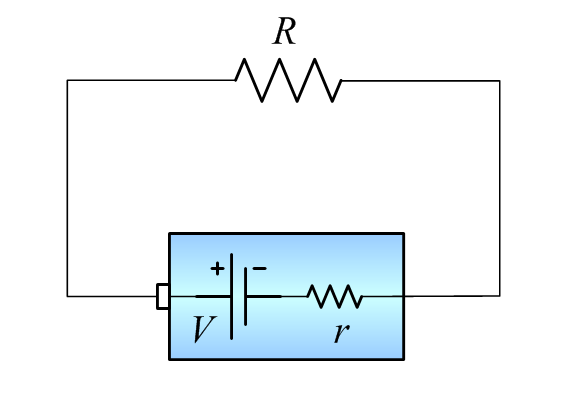
Quiz:
There is a circuit with a battery and a resistor, R. The original voltage of the battery is V and it’s connected to an internal resistor, r.

If you want to maximize the power consumed in the resistor R, what should you do?

1. Use a larger resistance of R.
2. Use a smaller resistance of R.
3. Make R equal to r.

Answer:
The power dissipated in the external resistor is given by $P = I^2 R$ in accordance with Ohm’s law.

The equivalent resistance of the circuit is $R+r$ because of series connections. The current is calculated as $I = V/R = \frac{V}{R+r}$.

Therefore, $P = \frac{V^2 R}{(R+r)^2}$      — (1)

You can see when $R \rightarrow 0$, the power will be zero; and when $R \rightarrow \infty$, the power will also be zero.

So the choices of 1 and  2 above are not the right ones. The answer must be 3, but how do you prove it?

Let’s use a trick. That is $(R+r)^2 – (R-r)^2 = 4Rr$. So we can have
$(R+r)^2 = 4Rr + (R-r)^2$ to plug in (1). The, just keep on calculating until you get something meaningful.

$P = \frac{V^2 R}{4Rr + (R-r)^2}$ $= \frac{V^2 R}{4r\left(R + \frac{(R-r)^2}{4r}\right)}$ $= \frac{V^2 }{4r}\frac{R}{R + \frac{(R-r)^2}{4r}}$ $= \frac{V^2 }{4r}\frac{1}{1 + \frac{(R-r)^2}{4Rr}}$ $= \frac{V^2 }{4r}\frac{1}{1 + \frac{(R-r)^2}{(R+r)^2 – (R-r)^2}}$ $= \frac{V^2 }{4r}\frac{1}{\frac{(R+r)^2-(R-r)^2+(R-r)^2}{(R+r)^2 – (R-r)^2}}$ $= \frac{V^2 }{4r}\frac{(R+r)^2 – (R-r)^2}{(R+r)^2}$ $= \frac{V^2 }{4r}\left\{ 1-\frac{(R-r)^2}{(R+r)^2}\right\}$

Now, you can notice when $R = r$, you will get the maximum power, $\frac{V^2 }{4r}$