Question:

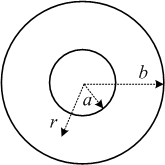
A toroid has \(N\) turns both sides carrying equal current \(I\). The inner and outer radii are \(a\) and \(b\), respectively. A distance \(r\) is supposed to be exact the middle between \(a\) and \(b\). Find the magnetic field at \(r\).

Answer:

From Ampere’s law, if inside the contour has a current $I$, we have the relationship:

\[  \oint \vec{B}\cdot dl = \mu_0 I  \]

The radius of the contour is \(r\) which encloses the current \(N\times I\). Therefore,

\[  B(2\pi r) = \mu_0 NI  \]

Recall that \(r=\frac{a+b}{2}\); thus, the magnetic field is

\[  B = \frac{\mu_0 NI}{\pi(a+b)}  \]