Question:

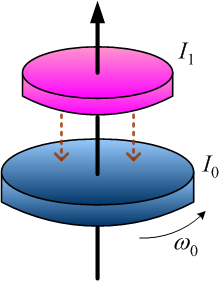
A solid cylinder with a moment of inertia, \(I_0\), rotates about its center at an angular velocity of \(\omega_0\). Another solid cylinder, which is initially rest, is put onto the rotating one gently. Both eventually rotate at an angular velocity, \(\omega_f\). Find the velocity of \(\omega_f\).

Answer:

The angular momentum is defined as the moment of inertia times its angular velocity:

\[  L = I\omega  \]

With the constant velocity, initial and final angular momenta should be conserved. Namely, the initial total momentum = the final total momentum. In this case, we have

\[  I_0 \omega_0 = (I_0 + I_1)\omega_1  \]

Then, solve for \(\omega_f\).

\[  \omega_f = \frac{I_0 \omega_0}{I_0 + I_1}  \]